The Slide Rule - hand held computation before there were hand held computers

Posted by: pkmurphy 11 years, 6 months ago

(0 comments)

In Tangible Bits: Beyond Pixels, Hiroshi Ishii tells of meeting an "abacus" when he was two years old. Speaking about himself in third person:

He could enjoy the touch and feel of the "digits" physically represented as arrays of beads. This simple abacus was not merely a digital computational device. Because of its physical affordance, the abacus also became a musical instrument, imaginary toy train, and a back scratcher. He was captivated by the sound and tactile interaction with this simple artifact.

I had a similar experience as a toddler in the 70s. I was investigating the drawers of my father's desk, when I found this strange device. It consisted of a cylinder with numbers written on it. There was also a black cover or cladding on top of the numbers that could be rotated around the gadget – but rotating would also force the cladding up and down the cylinder. I remember looking at the numbers, and trying to make sense of them. But I also recall enjoying playing with the cover, because it would make it spiral while being moved from one end or another.

Otis King's Patent Calculator Model L. Image taken from Retro Calculators

I don't know what happened to this contrivance. Did it get lost in the move from Canada to Australia, or did my father throw it out? It hardly matters. What interests me is what the machine was, and I didn't work that question out until years later. It was a slide rule. Most slide rules are flat (as will be shown below), but it appears I had got my hand on the rarer cylindrical variant. It could have been an original Otis King Patent Calculator, or it might be a cheaper variant after the patent expired. (All I've got is thirty year memories to go by.) What's a more important question to answer (because I don't expect everybody reading this to know) is: what's a slide rule?

This is a slide rule. Image taken from Wikipedia.

A slide rule is a mechanical, hand held device to enable users – mainly scientists and engineers – calculate with numbers. Most slide rules appear like three rulers stuck together, with the two slats at the top and the bottom fixed relative to each other, while the one in the middle can slide left and right. Slide rules could allow the user to perform several operations, the most important of which is multiplication. How does it work? To explain it, I'll start with the operation of addition, show how mechanical "manipulation" can add two numbers, and then move on to multiplication.

Let's say you are trying to add two numbers, such as 2 and 3. It's easy to do it with three normal rulers (slide rules are generally not used for this sort of thing). Take ruler 1, and measure 2 cm to point a. For ruler 2, you place the "0" at that point, and measure 3 cm from there to point b. If you take ruler 3, and place it at the "0" point of ruler 1, you find that 5 cm take you from there to point b. We have demonstrated that 2 + 3 = 5, which is wonderful. However, if you want to calculate 2 × 3 (which is 6), you're out of luck. You have to get the extra 1 cm from somewhere.

The trick to the slide rule is the logarithm. For any positive numbers x and y, log(xy) = log(x) + log(y). So you represent a number x on a slide rule not by a length of x cm, but a length of log(x) cm. The number 2 would be represented by 0.69 cm, 3 would appear as 1.10 cm, and 6 would measure out to 1.79 cm. (We can use other units of measurement and logarithmic bases as well, but let's stick with centimetres and base 10 for this exercise; it makes no difference.) The result is like a ruler; except that the spacing between consecutive integers gets smaller and smaller the higher the number goes. But that's what the logarithmic function does, and it works.

So how do people multiply two numbers? You read off the first number on the bottom slat (say, 2), slide the second slat to set its 1 to this number, and then move on to the second number on this slat (say, 3). The distance between this and the number 1 on the bottom slat indicates the value of the multiplication. Since 0.69 cm + 1.10 cm = 1.79 cm (which is how 6 is represented), we know that 2 by 3 is 6. If this doesn't make sense, look at the diagram. Or read the original Wikipedia article.

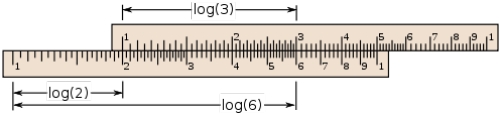
Slide rules in action: multiplying 2 by 3 on the device. Image also from Wikipedia.

Abacuses were brought up by Mr. Ishii above. How does a slide rule compare against an abacus, especially when considering "Tangible To Embodied Interaction"?

• Abacuses mainly deal with addition and subtraction, and there are techniques to use them for multiplication and division. Slide rules can be used for multiplication (as can be seen above), and by sliding a slat in reverse, division. By adding more numbers and lines, they can be also used for logarithms, exponentiation, and related operations like cube roots. Can you use them for adding and subtracting? I don't know – I think for those operations it would be more suitable to revert to paper and pen!
• Abacuses date from antiquity, and are still being used today in Asia and Africa. In contrast, slide rules were used over a shorter period. They were invented in the 1600s, and were used widely until handheld scientific calculators became common in the early 1970s.
• In Mark Weiser's model, slide rules require interactions at the inch level. Most devices are smaller than a foot, let alone a yard. They were designed to be held in the hand by engineers walking from project to project; most came with a nice case for carrying. Abacuses, in contrast, can be of any size, from tiny Soroban at an inch level, to desktop models at a foot level, and outdoor installments at the yard level. 
• You need direct manipulation to use both computational devices. For a normal slide rule, you need to slide the slats (or twist the "cladding") to the correct position to calculate, and for an abacus, you need to adjust the beads.
• The results of abacus computation are tangible and visual, and it is possible to "read" by touch. The results of slide rule computation are read by sight, but it is very hard to read the results by touch (unless your fingers are sensitive enough to feel the lines). In that respect, slide rules are intangible. It would be possible to add Braille markings to the numbers, but no-one has tried – and getting Braille on fractional results sounds like too much trouble.
• It is easier to add "visceral design" to an Abacus: colour the beads and the frame in whatever attractive colours suit you. It is not so easy with a slide rule: lines and numbers are organised in a very small area for visual reading. That limits designers to a number of colours (black) and contrasting backgrounds (white or yellow). That makes the devices very utilitarian to look at, but not exactly "fun".

Computing has changed immensely in my life. When I was born, slide rules were still in use. The electronic calculator came out not long afterward, and by the time I came of age, calculators were common, and slide rules were rare outside of museums. Another twenty years, and mobile devices support their own calculator apps, making the need to buy calculators unnecessary, except possibly for university exams. I thought it was necessary to acknowledge these changes. That's why I wrote my last "Social and Mobile Computing" essay about the slide rule – it is an example mobile computing, if not social computing. I wanted to go backwards in time for once.

• Tags:
• DECO7350

• ← A not so small Foursquare review
• An email to multilevel marketeers →